国際数学オリンピックについて

国際数学オリンピックとは

国際数学オリンピック（IMO）は、大学入学前の生徒が数学の問題６問を解くことで競い合うコンテストであり、国際科学オリンピックの中では最も歴史がある（第1回は1959年にルーマニアで開催）。現在は百カ国以上が参加、各国から選手6人を含む選手団が送られる（選手の選抜は各国別）。コンテストは2日間実施され、各日3問を4時間30分で解き、1問7点、42点満点として採点される。出題分野は、①平面幾何、②整数論、③代数、④組合せ論の４分野で、立体幾何、三角関数、微分・積分、確率・統計等は含まれない。すなわち、日本の大学受験数学とは範囲は重なるが、頻出分野は異なる。各日3問ずつの問題は、問1、問2、問3（2日目は問4、問5、問6）の順に難易度が増し、それぞれ「1番級」「2番級」「3番級」などと呼ばれることがある。なお、いずれの問も普通の大学受験生にとっては時間を費やす割に解答を導くことが出来ない「効率の悪い」問題ばかりであり、1番級の問を完答するにも一定の訓練が必要である。スコアは個人別に集計、参加者の半数弱がメダリストとなり、金・銀・銅メダリストの人数比は1:2:3である。メダルが授与されなかった場合でも、1問完答（部分点なしの7点）で特別賞（Honorable mention）が授与される。

国別順位では、中国チームの最多得点回数が最も多く、近年は中国チームに加え、米国チーム、韓国チームが最多得点を得ている。日本チームは、2009年ドイツ大会の2位が最高順位である。なお、出題される問題の決定方法や採点方法については、参考に掲げた秋山論文に詳しい記載がある。国別順位やチーム内メダリストの数には、選手の力量だけでなく（あるいはそれ以上に）選手団の団長およびコーディネーターの力量が寄与する。

IMOメダリストからはフィールズ賞 *1受賞者が多数輩出されている。例えば、ポワンカレ問題を解決したグレゴリー・ペレルマン氏は1982年に参加、満点（世界1位）で金メダルを授与されている*2。また、昨年フィールズ賞を受賞したピーター・ショルツェ氏は2004年から2007年まで計4回参加し、金メダルを3回、銀メダルを1回授与されている*3。

日本数学オリンピック

つぎにIMOに参加する日本選手の選考過程についてみる。日本は1990年の北京大会より参加しており、昨年（2018年7月）まで29年間参加し、延べ174人の選手を送り出している。

選手となるためには、まず1月上旬に開催される日本数学オリンピック（JMO）予選（または日本ジュニア数学オリンピック（JJMO）予選）に参加する必要がある。参加資格は、予選実施時点において「大学教育（またはそれに相当する教育）を受けていない20歳未満の者」とされており、高等学校卒業者であっても、大学に入学していなければ参加可能である（JJMO予選の参加資格は、予選実施時点において「中学3年生以下の者」。）*4。この予選では12問を3時間で解き、1問1点、12点満点として採点される。すなわち、予選では解答に至る過程は一切問われず、解答が合っていれば得点を得る。問題の難易度は、大学入試標準程度の問題から正解者が見込めないような難問までであり、問題の並びは概ね難易度順（易問→難問）である。例年、上位約200名がAランクとなり本選に進むが、ボーダーの得点は5～8点とばらつきがある。

ちなみに2019年は（欠席者315名を除き）4108人が予選に参加、303人がAランク（ボーダー5点）となり、予選免除者1名を加え304人が本選に進んだ。得点別人数は、Aランク者の氏名と伴に国際オリンピック財団のサイト（下記参考を参照）に掲載されており、ボーダーの得点5に対し、平均点は2.44、標準偏差は1.34となる。分布から明らかなとおり、既に予選の時点でAランク者は正規分布のテール部分に位置している。多くの人に馴染みのある偏差値を仮に当てはめると、最高点8点は91.42、ボーダーの得点5点は69.06となる。

翌2月に開催される本選では5問を4時間で解き、1問8点、40点満点として採点される。予選とは異なり、解答に至る過程が重要となり部分点もある。予選とは逆に、解答のみ合っていても、過程に誤りがあればその段階で得点に至らない場合もある。経験者であっても、自己採点と実際の得点が一致しないことがあるとのことである。問題の難易度は予選よりも高く、大学入試難問程度の問題から正解者が見込めないような難問までとなる（問題の並びは予選に同じ）。予選Aランク者等約200名（2019年は304名）から約20名（同23名）が金・銀・銅賞および優秀者として表彰される。また、最高得点者には川井杯*5が授与される。予選とは異なり、金・銀・銅賞および優秀者の氏名のみが公表され、得点別人数やボーダーの得点は公表されない。なお、年によって難易度の違いはあるものの、一般的には2問完答、16点前後がボーダーとのことであり、正規分布のテール部分に位置する者同士の競争とはいえ、得点を得るに至らない者も相当数いると推察される。

参考として掲げた田村論文では、アメリカ初等中等教育法に準拠し、日本において「数学的才能者」（gifted and tarented）を定義する一つの基準としてJMO本選表彰者を上げている。現在、受験者の数は当該論文の執筆時（2011年頃）から倍増しており、その基準は、当時よりも厳しいものとなっていると考えられる。

JMO本選表彰者約20名に、JJMO本選における銀賞以上受賞者5名を加えた約25名が、3月に国立青少年オリンピックセンターで開催される春合宿に参加し、IMO日本代表選手の最終選考に臨む。ただし、JMO本選表彰者のうち次年度大学進学が見込まれる高3生・高卒生は、（IMO開催が7月であるため）春合宿には参加できない。春合宿の4日間、各日3問を4時間30分で解き、1問7点、84点満点として採点される。問題の難易度はさらに高くなり、JMO本選の標準レベルの問題から正解者が見込めないような難問までとなる。この時点で、問題の難易度はIMOとほぼ同等のものとなる。上位6名が、IMO日本代表選手に選出される。

IMO日本代表選手の学校別人数および進路

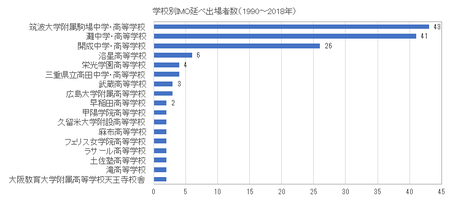
最後に、過去29年間、延べ174人の学校別人数（延べで2名以上出場実績のある17校）をみると、つぎのようになる。

筑駒43人、灘41人、開成26人を除くと、全て出場者数は一桁のオーダーであり、当該3校の全174人に占める割合は63.22％となる。IMO出場者の出身校は明らかに偏っており、加えて女子の出場者は延べ3人と、性別にも大きく偏る。また、直近10年間に限ってみても、当該3校の全60人に占める割合は65.00％と、偏った傾向に違いはみられない。なお、東京大学理科三類（定員100名弱）合格者の学校別人数は、ここ数年、灘、筑駒、開成、桜蔭の4校がほぼ固定的に上位を占めているが、筑駒、灘、開成の3校は、これとも重なる。

また、1990年から2005年までのJMO予選通過者1,063人に対し、文部科学省科学技術政策研究所が行ったアンケート調査（回収率28.3％）によると、大学で数学を専攻した者は、IMO出場者では高校生を除く13人中6人と大半を占めるが、全体でみると、回答があった大学・大学院生、社会人240人中48人で医学系進学者（49人）よりもやや少ない。とはいえ、それ以外の者の大半は理学、工学、情報工学等の理数系を専攻しており、必ずしも「数学オリンピック参加者の多くは、数理系ではなく、医学系に進学してしまう」という通念は当てはまらないとしている（下記参考を参照）。

最後に、小島寛之『数学は世界をこう見る数と空間への現代的なアプローチ』から、IMOに出題された問題に関する興味深い話を引用する。

　この五角形の問題（引用者注：1986年IMOワルシャワ大会）を最後にもってきたのは、実は、全く別のルートからこの問題の話を耳にしたからです。
　筆者の友人のある数学者から、この問題と全く同じ問題が、最先端の研究の中に現れた、ということを教えてもらったのです。彼が新しい論文についてゼミで検討をやっているとき、ある定理の証明の際にこの問題が出現したそうです。（中略）
　この問題が出現したのは、「代数幾何」という分野の「中山の定理」の証明の中です。中山昇という数学者が提出したものであり、1992年にプレプリントが出ています。
　（中略）
　筆者はその数学者の友人に、「誰か外国の数学者が全く同じ研究をしていて、そこからこの問題を数学オリンピック用に出題したのではないか」と尋ねたのですが、彼の返答は「まずそれは考えられない」ということでした。出題時には中山はまだ発表をしていなかったし、仮に他の学者がこの成果を得ているなら、彼らの耳に入らないはずはない、と彼はいいました。とすれば、物理関係か何かの全く異なる分野において同じ問題を考えていた数学者がいる、ということになります。これはとても不思議な話です。
　この一件は、IMOの問題が単なるパズルではなく、現代数学と一緒に脈動していることをよく物語っていると思います。（以下略）